#2468 문제는 그래프 이론, 부르트포스 방법 등으로 풀 수 있겠지만, 전 정렬을 이용한 탐욕 알고리즘을 이용해서 풀었습니다.
어쩌다 보니, 푼 사람 내에서 상위권에 있다보니 제 소스 참조횟수가 많은 문제가 되었네요.
https://www.acmicpc.net/problem/2468
2468번: 안전 영역
재난방재청에서는 많은 비가 내리는 장마철에 대비해서 다음과 같은 일을 계획하고 있다. 먼저 어떤 지역의 높이 정보를 파악한다. 그 다음에 그 지역에 많은 비가 내렸을 때 물에 잠기지 않는
www.acmicpc.net

제가 생각한 것은 단순합니다. 일단 지대가 높은 것부터 낮은 순으로 정렬을 합니다. 지대가 가장 높은 곳은 비가 가장 많이 왔을 때에도 안전지대가 되겠죠. 그리고 그 영역의 개수는 상호 배타적 집합(disjoint set)으로 묶어서 사용했습니다. 비의 양이 적어지면서 안전지역은 많아지면서 서로 연결되는 구조를 갖게 됩니다.
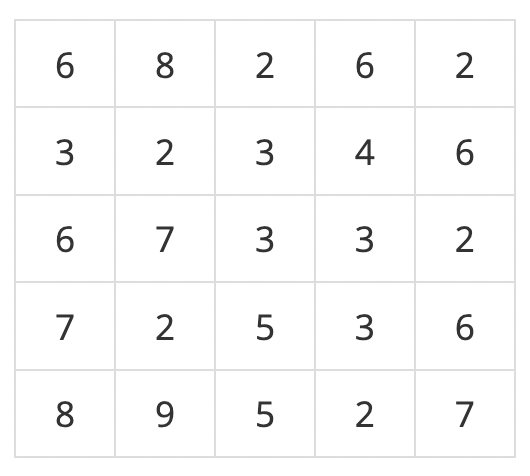
초기에 위와 같은 지대별 높이가 주어집니다. 그러면 높이가 가장 높은 곳은 9이고, 가장 낮은 곳은 2가 됩니다.
가장 높은 높이인 9까지 물이 찼을 때에는 오직 한군데만 안전지대가 됩니다.
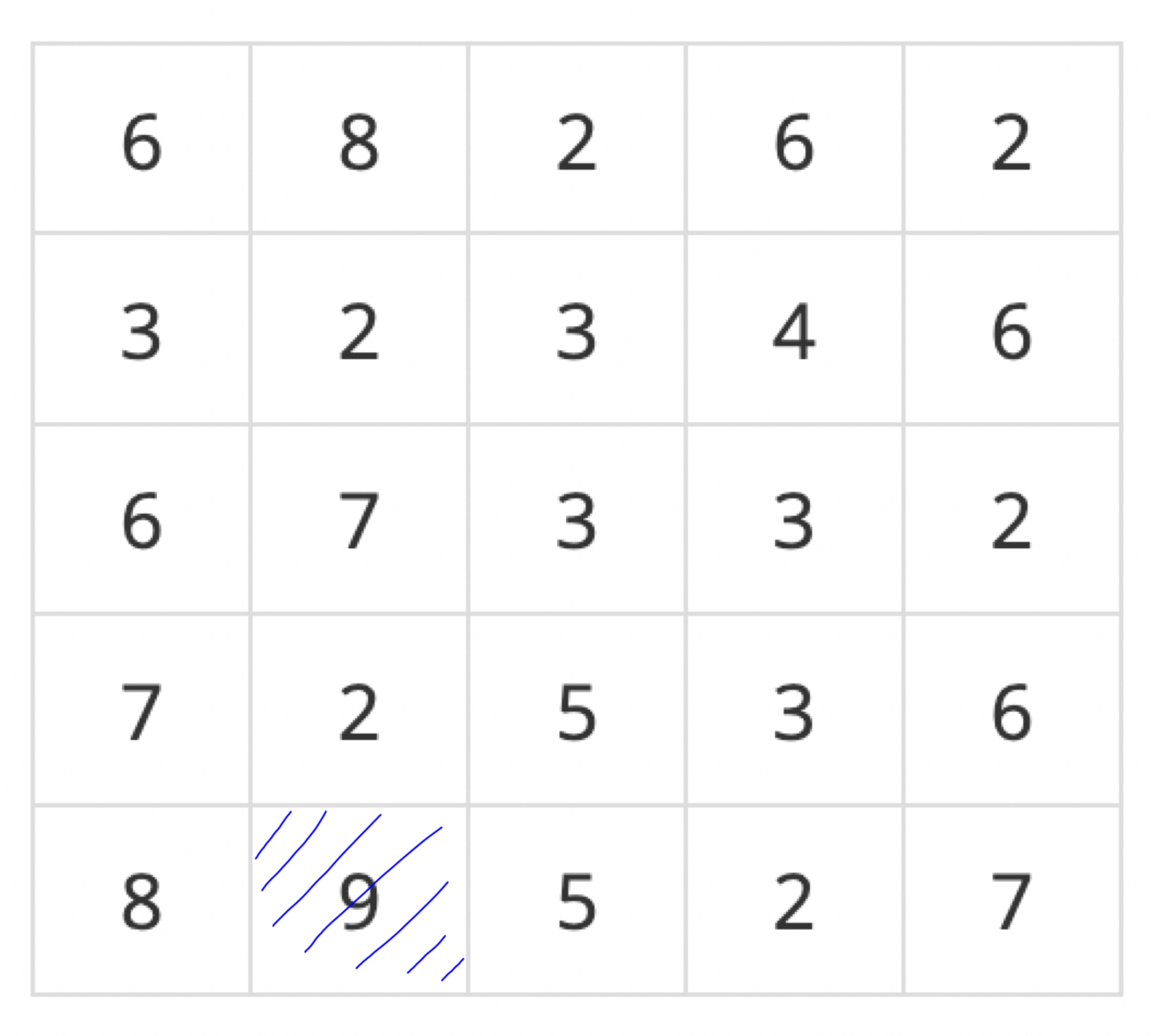
다음은 8일 때입니다. 왼쪽 아래 8은 주변에 9라는 집합이 있으니, 이 집합에 합쳐집니다. 위에 있는 8은 새로운 집합이 생성되어서 안전지대는 2가 됩니다.

다음은 7에 대해서입니다. 왼쪽 아래에 있는 7은 8과 인접해서 같은 집합으로 흡수됩니다. 그 외에 7들은 모두 별개의 집합이 되어 총 안전지대의 수는 4가 됩니다.
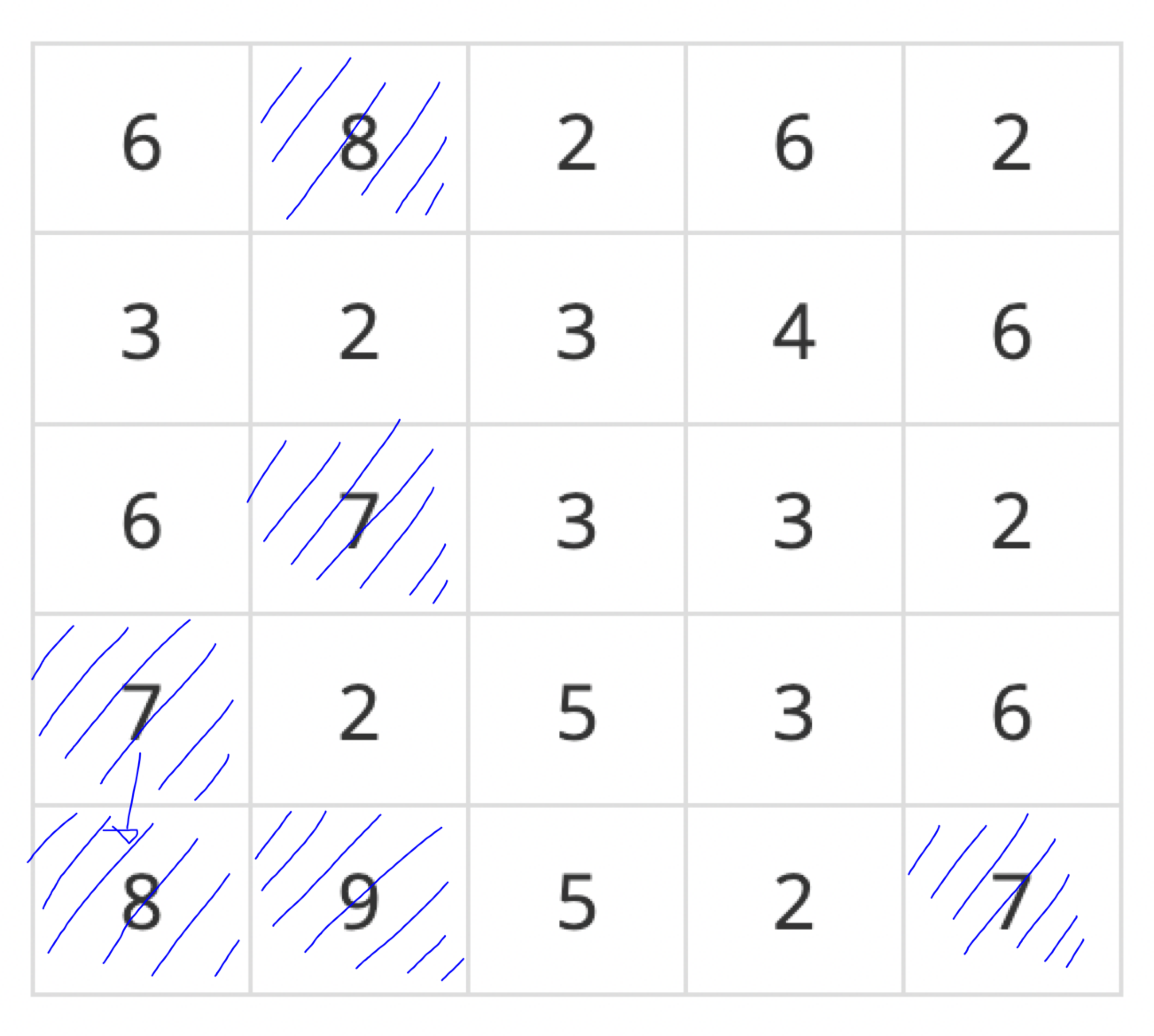
다음은 6에 대해서입니다. 안전지대의 수는 5개입니다. 여기서 주의할 것은 왼쪽 위에서 세번째 6입니다. 이 것에 의해서 두개의 집합이 결합을 하게 됩니다.

이런식으로 5, 4, 3, 2 순으로 처리를 하면, 그래프 이론을 사용하지 않고 원하는 결과를 얻을 수 있습니다.
깊이 우선 탐색이나 너비 우선 탐색이 \(O(N^2)\)이 되기 때문에 높이의 종류 D에 대해서 \(O(DN^2)\) 알고리즘이 됩니다.
제 경우에는 정렬 알고리즘에 대한 것만 따지기 때문에 \(O(N^2 \log N)\)이 됩니다.
제가 작성한 소스입니다.
//------------------------------------------------
// baekjoon #2468
// - by Aubrey Choi
// - created at 2019-09-09
//------------------------------------------------
#include <stdio.h>
#include <algorithm>
int map[10000], v[10000], p[10000];
int getroot(int n)
{
if(p[n]==-1) return -1;
while(p[n] != n) n = p[n];
return n;
}
int main()
{
int n, n2, max=0, c=0;
scanf("%d",&n); n2=n*n;
for(int i=0; i<n2;i++) { scanf("%d",map+i); v[i]=i; p[i]=-1; }
std::sort(v,v+n2,[](int a, int b) { return map[a]>map[b]; });
for(int i=0;i<n2;)
{
for(int t=map[v[i]];i<n2&&map[v[i]]==t;i++)
{
int r = v[i], x[4], cx=0;
if(r%n>0&&p[r-1]!=-1) x[cx++]=p[r-1];
if(r>=n&&p[r-n]!=-1) x[cx++]=p[r-n];
if(r%n<n-1&&p[r+1]!=-1) x[cx++]=p[r+1];
if(r<n2-n&&p[r+n]!=-1) x[cx++]=p[r+n];
if(cx==0) { p[r]=r; c++; continue; }
p[r] = getroot(x[0]);
for(int j=1;j<cx;j++)
{
int t=getroot(x[j]);
if(t!=p[r]) {c--; p[x[j]]=p[t]=p[r];}
}
}
if(c>max) max=c;
}
printf("%d\n", max);
}
'Programming > BOJ' 카테고리의 다른 글
| [C/C++] 백준 #2491 수열(구현) (0) | 2023.05.23 |
|---|---|
| [C/C++] 백준 #2482 색상환(동적 계획법) (2) | 2023.05.22 |
| [C/C++] 백준 #2458 키 순서(플로이드 워샬) (2) | 2023.05.11 |
| [Python] 백준 #2457 공주님의 정원(탐욕 알고리즘) (2) | 2023.05.08 |
| [C/C++] 백준 #2448 별 찍기 - 11(재귀 함수) (0) | 2023.05.06 |




댓글