비트단위 연산은 알고리즘에서도 많이 사용할 수 있는데, 이제까지 봤던 간단한 형태의 연산에서 이제는 알고리즘이라는 것을 적용해보고자 합니다. 일단 보수라는 것을 살펴보도록 할께요. 보수(Complement)라는 것은 반대되는 수를 말합니다. 우리는 알게모르게 보수라는 개념을 많이 사용하고 있습니다. 34-16 을 계산할 때에도 보수라는 개념을 사용할 수 있습니다. 14-6=8 이라는 개념보다는 보수를 사용하면 뺄셈을 덧셈으로 대치할 수 있으니까요. 14-6=10+4-6=(10-6)+4=4+4=8 이란 개념이죠. 여기서 4는 6에 대한 10의 보수입니다. 이진수에서도 보수를 많이 사용하는데 크게 두가지의 보수를 많이 사용합니다. 1의 보수와 2의 보수입니다. 엄밀하게 이야기한다면 -1의 보수와 0의 보수라 이야기하는 것이 더 적당할 듯 합니다.
1의 보수는 모든 비트를 반전하는 것입니다. 달리 말하면 -1에서 주어진 수를 빼었다고 할 수 있습니다. 2의 보수는 2의 멱승수로부터 주어진 수를 빼는 것을 말합니다. 이것을 식으로 표현하면 다음과 같습니다. x' 을 x에 대한 1의 보수라고 표현하도록 할께요.
\[ x' = x \odot -1 ~~~ -x = x' + 1 ~~~ -x = ( x – 1 )' \]
이렇게 식으로 표현했지만, 실제 우리는 이 식을 바로 유추하기에는 어려움이 있습니다. 그래서 0부터 7까지의 숫자에 대해서 각각의 값들을 유추해보고자 합니다. 편의상 모든 수는 2진수로 표현했습니다.
|
X |
X' |
-X |
X-1 |
|
0000 |
1111 |
0000 |
1111 |
|
0001 |
1110 |
1111 |
0000 |
|
0010 |
1101 |
1110 |
0001 |
|
0011 |
1100 |
1101 |
0010 |
|
0100 |
1011 |
1100 |
0011 |
|
0101 |
1010 |
1011 |
0100 |
|
0110 |
1001 |
1010 |
0101 |
|
0111 |
1000 |
1001 |
0110 |
표에서 보면 위에 적은 식의 규칙이 성립함을 알 수 있습니다. 일단 이것을 잘 이해하게 되면, 이것을 이용해서 우리가 간단한 알고리즘을 만들 수 있습니다.
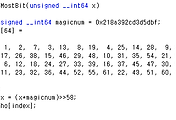
가장 오른쪽 1인 비트 알아내기
가장 오른쪽 1인 비트를 알아내기 위해서는 위에서 설명한 공식이 필요합니다. 보다 일반화하기 위해서 우리는 다음과 같은 일반화된 식으로 표현하고자 합니다. 여기서는 b+1번째 처음으로 1인 비트가 나타난 경우입니다.
\[ x = ( \alpha 01^a 10^b )_2 \]
그럼 이 x 를 이용해서 여러 가지 연산을 해보도록 합니다. 기본적인 연산은 표에 있는 연산입니다.
\[ x' = ( \alpha ' 10^a 01^b )_2 \]
\[ -x = ( \alpha ' 10^a 10^b )_2 \]
\[ x-1 = ( \alpha 01^a 01^b )_2 \]
이 식을 기억하면, 여러 가지 연산을 통해서 우리가 얻을 수 있는 다양한 패턴들을 만들 수가 있습니다.
-
가장 오른쪽에 있는 1인 비트 제거 : \( x \& ( x – 1 ) = ( \alpha 01^a 00^b )_2 \)
-
가장 오른쪽에 있는 1인 비트만 남김 : \( x \& –x = (…0 00^a 10^b )_2 \)
-
가장 오른쪽에 있는 연속된 0인 비트들을 1로 변경 : \( x' \& (x-1) = (…000^a 01^b )_2 \)
-
가장 오른쪽에 있는 연속된 1인 비트들을 0로 변경 : \( (( x | (x-1))+1) \& x = (\alpha 00^a 00^b )_2 \)
사실 우리가 얻고자 하는 답은 두 번째 \( x \& –x \)입니다. 이를 이용하면 가장 오른쪽에 있는 1인 비트를 제외하고 모든 비트들을 0으로 만듭니다. 의심이 가신다면 직접 위의 표에서 계산을 해보시길 바랍니다.
그러나 이것만 가지고는 부족합니다. 실제 우리가 필요한 것은 바로 b가 얼마인 가입니다. 비트연산만 가지고 작업한 것은 단순하게 가장 오른쪽에 있는 비트 값이 1인 비트만 제외하고 모든 비트들을 0으로 만든 것에 불과합니다.
'Programming > Algorithm' 카테고리의 다른 글
| Bitwise operation V (0) | 2011.09.27 |
|---|---|
| Bitwise operation IV (0) | 2011.09.26 |
| Bitwise operation II (0) | 2011.09.22 |
| Bitwise operation I (0) | 2011.09.21 |
| 수, 거듭제곱, 로그 (0) | 2011.09.21 |
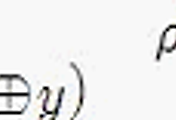

댓글