Programming/Project Euler118 [C/C++] 프로젝트 오일러 #42 : 삼각수 단어 이 문제는 알고리즘이 크게 필요하지는 않습니다.그래서인지 문제의 난이도는 5%입니다. 어떤 단어의 알파벳 값을 다음과 같이 정의할 수 있습니다. 각 알파벳은 A=1, B=2, C=3, …, Z=26의 값을 가지며, 단어의 알파벳 값은 각 문자에 해당하는 숫자를 더한 값입니다. 예를 들어, “SKY”라는 단어는 S=19, K=11, Y=25이므로, 알파벳 값은 19 + 11 + 25 = 55가 됩니다.한편, 삼각수(triangle number)는 다음과 같은 공식으로 계산할 수 있습니다.Tn=n(n+1)2 여기서 n 은 자연수이며, 예를 들어 첫 몇 개의 삼각수는 1, 3, 6, 10, 15, 21, … 과 같이 됩니다.주어진 단어 리스트에서 단어의 알파벳 값이 삼각수와 같은.. 2016. 5. 24. [C/C++] 프로젝트 오일러 #41 : 팬디지털 소수 이 문제의 난이도 5%입니다. 그렇게 어렵지 않은 문제이죠.문제를 살펴보면 다음과 같습니다.우리는 1부터 n까지 정확하게 한번씩만 사용한 n자리 숫자가 있다면, 이것을 팬디털(pandigital) 숫자라고 부릅니다. 예를 들어서 2143은 4자리 팬디지털 숫자이면서, 또한 소수입니다.가장 큰 n자리 팬디지털 소수는 얼마일까요?일단 팬디지털이라는 것을 알았으면, 우리는 간단하게 1~9까지 한번만 사용해서 이 숫자를 구하면 됩니다.팬디지털을 만들 수 있는 가장 큰 자릿수는 9자리입니다. 왜냐하면 그 이상부터는 두자리숫자가 될 수밖에 없기 때문에 팬디지털 정의에 어긋납니다.프로그램은 9자릿수부터 만들 수 있는 모든 팬디지털수를 만듭니다. (사실 이것을 1부터 n까지 배열하는 순열수입니다.) 순열 수 중에 사실.. 2015. 10. 27. 515. 프로젝트 오일러 #515 : 불협화음 숫자들 문제 : Let d(p,n,0) be the multiplicative inverse of n modulo prime p, defined as n × d(p,n,0) = 1 mod p. Let for k ≥ 1.Let for all primes a ≤ p = 0 ) { int64_t r = t; t = -t*rec[count]+s; s = r; } t = (t>0)?t:p+t; return t; } 사실 인터넷에 뒤져보면, 아마 역원 구하는 알고리즘이 나와있을 것 같은데, 저는 알고리즘을 수학적 방법으로 제가 알고 있는 그대로를 구현했기 때문에 성능은 보장하지 못 합니다. 그리고 오버플로우가 발생할 수도 있고요. 이렇게 하면, 역원을 구하는 것과 d(p, n, 0)의 갯수를 세는 것이 다 되었습니다.그런.. 2015. 5. 12. 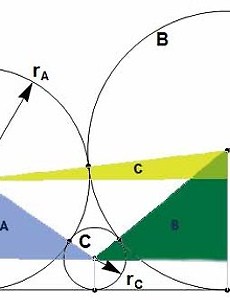[C/C++] 프로젝트 오일러 #508 : i−1 진법 표시하기(수학) 이번 문제는 아직까지도 푼 사람이 100명이 넘지 않는 문제네요. 그만큼 복잡할 수 있는 문제이므로, 블로그에 자세한 풀이법을 적기는 힘드네요. 문제는 주어진 범위안의 복소수를 i−1 진법으로 표현했을 때, 1의 갯수의 총 합입니다. 복소수에 보면, 정수가 계수인 복소수들이 자연수의 소수처럼 취급될 수 있는 것들이 있습니다. 이것들을 일반적으로 가우스 소수라고 합니다. 가우스 소수는 몇가지 법칙이 있는데요. 기본적으로 자연수의 소수에서 갈라지게 됩니다. 자연수의 소수 중 4k+3 형태의 소수는 자체로 가우스 소수가 됩니다. 즉, 3, 7, 11, 19, .. 등입니다. 그 외의 자연수 소수들은 모두 복소수 형태의 가우스 소수로 나누어지게 됩니다. 예를 들어서 소수 2는 \( \pm 1 \p.. 2015. 5. 2. 510. 프로젝트 오일러 #510 : 원의 접선 중학수학 시절에 기하가 나오면, 보조선만 잘 그리면, 기하 문제는 왠만하면 풀린다는 것이죠. 이 문제도 역시 보조선을 잘 그리면 될거라고 생각합니다. 보조선을 그린 이미지를 보시면, 원 A에서 선 L에 수선을 내리고, 원B에서 선 L에 수선을 내리고, 원 A의 중심에서 L과 편행하고 선을 긋고, 원 C의 중심에서 L과 평행하게 선을 긋습니다. 그러면 그림과 같이 A, B, C 라는 삼각형을 얻습니다. 이 문제의 풀이는 바로 이 세개의 직각삼각형에서 출발합니다. 직각삼각형이므로 당연히 피타고라스 법칙이 성립합니다. 그런데, 삼각형 A의 밑변, 삼각형 B의 밑변, 삼각형 C의 밑변이 자연수라고 생각할 수 있는 근거가 그림상에는 전혀 없습니다. 당연히 A, B의 밑변의 합은 C의 밑변의 길이와 같다는 것은 알.. 2015. 4. 22. [C/C++] 프로젝트 오일러 #40 : 챔퍼나운 수 문제 요약 챔퍼나운 수는 0.123456789101112131415… 와 같이 자연수를 차례대로 이어붙여서 만든 무리수입니다. 문제에서는 이 상수에서 특정 위치에 있는 숫자들을 찾아 곱한 값을 구하는 것이 요구됩니다. 예를 들어, 소수점 아래 1번째 자리의 숫자는 1, 2번째는 2, 10번째는 1과 같이 특정 위치에서 숫자를 확인할 수 있습니다. 이러한 방식으로 문제에서 요구하는 여러 개의 특정 위치에 있는 숫자들을 추출하고, 이들을 곱하여 최종적으로 그 값을 도출해야 합니다.챔퍼나운수는 수론에서 무리수이자 초월수인 상수를 정의한 것입니다. 십진법이라면, 1, 2, 3, 4, 5, ... 를 세듯이 소수점 이하에 배열을 한 것입니다. 10진법 챔퍼나운 수는 다음과 같습니다.\[ C_{10} = 0.123.. 2015. 4. 21. 이전 1 ··· 10 11 12 13 14 15 16 ··· 20 다음 728x90
