펠의 방정식(Pell's Equation) - 3

Pell's equation

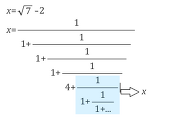
연분수 전개로 당연한 식이지만, 다음과 같은 형식의 식을 만들었습니다.

$$\sqrt{d}=\frac{r+s\sqrt{d}}{p+q\sqrt{d}}$$

 

첫번째로는 과연 저 형식의 식과 펠의 방정식은 무슨 관계인가입니다.

$d=7$일 때, $p=1,q=1,r=7,s=1$라는 것도 저 식을 만족합니다. 왜 하필이면, 복잡한 연분수 계산을 통해서 저 수를 얻어야 하는 것입니다. 그리고 펠의 방정식과 무슨 관계인가입니다.

 

위 식에서 분모를 유리화하면 다음과 같은 식을 얻습니다.

$$\sqrt{d}=\frac{r+s\sqrt{d}}{p+q\sqrt{d}}=\frac{pr-dqs+(ps-qr)\sqrt{d}}{p^2-d{q}^2}$$

 

분모를 유리화하면 분모는 정수가 됩니다. 좌변과 우변이 같게 되기 위해서는 분자는 제곱근만 남는 것이 마땅합니다. $ps-qr=1$ 이 된다면, 분모도 1이 되어야 합니다. 즉, $ps-qr$ 이 1이 된다면, 분모도 1이 되어서 바로 펠의 방정식을 만족하게 됩니다.

$$\sqrt{d}=a_0+\frac{h_{e-2}+k_{e-2}\sqrt{d}}{h_{e-1}+k_{e-1}\sqrt{d}}$$

 

우리가 연분수로부터 얻은 위 식을 연분수의 점화식을 이용해서 알아보도록 하겠습니다.

$$ps-qr=h_{e-1}{k}_{e-2}-k_{e-1}{h}_{e-2}$$

$$h_{-2}=0,h_{-1}=1,k_{-2}=1,k_{-1}=0$$
$$h_n=a_n{h}_{n-1}+h_{n-2},k_n=a_n{k}_{n-1}+k_{n-2}$$

$$\sqrt{d}=[a_0;(a_1,a_2,\dots ,a_e)]$$
i) if $n=1$,
$$h_0=a_0,h_1=a_0+1,k_0=1,k_1=1⟹ps-qr=a_0-a_0\cdot 1-1=-1$$
ii) if $n=t$, Assume that $ps-qr=h_{t-1}{k}_t-k_{t-1}{h}_t=(-1{)}^t$
iii) if $n=t+1$,
$$\begin{array}{rl}ps-qr& =h_t{k}_{t+1}-k_t{h}_{t+1}\\ & =h_t(a_t{k}_t+k_{t-1})-k_t(a_t{h}_t+h_{t-1})\\ & =a_t(h_t{k}_t-k_t{h}_t)+h_t{k}_{t-1}-k_t{h}_{t-1}=(-1{)}^{t+1}\end{array}$$

 

귀납법적으로 보면, 연분수 전개에서 항상 $ps-qr$ 은 -1 또는 1임을 알 수 있습니다. 즉, 펠 방정식은 연분수 전개의 주기 $e$가 짝수라면, 1을, 홀수라면 -1을 만든다는 것을 알 수 있죠.

그래서 N이 1인 경우에 다음과 같은 해를 얻을 수 있습니다.

1) 연분수의 주기가 짝수이면, $x=h_{e-1},y=k_{e-1}$ 이 하나의 해이다.

2) 연분수의 주기가 홀수라면, $x=h_{2e-1},y=k_{2e-1}$ 이 하나의 해이다.

또한 $x=t_1,y=u_1$ 이 해라면, $x+y\sqrt{d}=(t_1+u_1\sqrt{d}{)}^n$ 을 만족하는 모든 (x, y)쌍들도 해가 됩니다.